
soal persamaan garis singgung melalui titik di luar lingkaran dan pembahasannya dengan 2 cara
Blog Koma - Persamaan garis singgung lingkaran merupakan suatu garis yang menyinggung suatu lingkaran. Untuk memudahkan dalam mempelajari persamaan garis singgung lingkaran, sebaiknya baca dulu materi "persamaan lingkaran".Ada tiga jenis yang diketahui dalam menentukan persamaan garis singgung lingkaran, yaitu : Garis Singgung yang Melalui Suatu Titik pada Lingkaran, Garis Singgung Melalui.

Cara Mudah Menentukan Persamaan garis singgung kurva y= ax²+bc+c dititik (x,y) Simple Konsep
Untuk langkah-langkah menggunakan Cara 2, yakni: Eliminasikan persamaan garis y-y1 = m(x-x1) dengan persamaan garis singgung sehingga diperoleh m; Substitusikan m ke persamaan garis; Baca juga: Cara Menentukan Persamaan Garis Singgung Lingkaran. Contoh soal . Persamaan lingkaran yang berpusat di (1,4) dan menyinggung garis 3x-4y+3 = 0 adalah.

Foto Cara Menentukan Persamaan Garis Singgung Lingkaran
Cara Menentukan Persamaan Garis Singgung Lingkaran. Kompas.com - 10/03/2023, 19:30 WIB. Retia Kartika Dewi, Serafica Gischa . Tim Redaksi. Retia Kartika Dewi. Tentukan persamaan garis singgung yang melalui titik (2,2) pada lingkaran x²+y²=8! Jawab: Pertama, periksa terlebih dulu apakah titik (2,2) terletak pada lingkaran x²+y²=8 atau.
Persamaan Garis Singgung Lingkaran Pada Matematika
Pengertian Garis Singgung. Dalam ilmu geometri, garis singgung atau biasa disebut juga garis tangen kurva bidang pada titik yang diketahui ialah garis lurus yang "hanya menyentuh" kurva pada titik tersebut. Leibniz mendefinisikan bahwa suatu garis singgung sebagai garis yang melalui sepasang titik tak hingga dekat pada kurva.

Cara Mudah Menentukan Persamaan Garis Singgung Lingkaran dengan Gradien YouTube
Titik di luar lingkaran (k > 0) Tips dan Trik Menjawab Soal Garis Singgung Lingkaran. Soal 1: Persamaan garis singgung melalui titik. Soal 2: Persamaan garis singgung memotong sumbu -Y. Soal 3: Persamaan garis singgung yang diketahui nilai jari-jari dan koordinat titik potongnya.

Contoh Soal Persamaan Garis Singgung Lingkaran Jika Diketahui Gradiennya Berbagai Contoh
Rumus Persamaan Garis Singgung. Setelah mengetahui pengertian dan langkah penyelesaiannya, kita masuk ke pembahasan rumus supaya bisa mendapatkan nilai persamaannya.. Untuk mendapatkan gradien garis (m), ada beberapa cara sebagai berikut: Jika y = ax + b, maka gradien garisnya bisa dicari dengan m = a. Jika ax + by + c = 0, maka gradien.

Persamaan Garis singgung Trigonometri Angela Veda YouTube
Setelah mengetahui gradien garis, langkah berikutnya adalah menentukan persamaan garis singgung. Persamaan garis singgung memiliki bentuk umum y = mx + c, di mana m adalah gradien dan c adalah konstanta. Dalam kasus persamaan garis singgung, kita memiliki gradien yang sudah kita ketahui (m) dan titik yang sudah kita ketahui (x1, y1).
Contoh Soal Persamaan Garis Singgung Lingkaran Jika Diketahui Gradiennya Berbagai Contoh
Persamaan garis singgungnya: Bentuk. Persamaan garis singgungnya: Contoh Soal: Persamaan garis singgung yang melalui titik (-1,1) pada lingkaran adalah.. Jawab: Dari soal diatas diketahui persamaan lingkaran nya adalah dengan A = -4, B = 6 dan C = -12 dan . PGS adalah. Jadi persamaan garis singgungnya adalah.

Cara Menentukan Persamaan Garis Singgung Dalam Trigonometri YouTube
Soal Latihan dan Pembahasan Persamaan Garis Singgung Lingkaran. Untuk menambah pemahaman kita terkait Lingkaran, khususnya Persamaan Garis Singgung Lingkaran ini, mari kita simak beberapa soal latihan di bawah ini. Soal latihan kita pilih dari soal latihan pada Modul Lingkaran Matematika SMA Kurikulum 2013.. Untuk soal Lingkaran yang sudah pernah diujikan pada seleksi masuk Perguruan Tinggi.
Video belajar Persamaan Garis Singgung Lingkaran yang Berpusat di Titik O (0,0) yang Berjari
Pelajaran, Soal & Rumus Persamaan Garis Singgung Lingkaran Diketahui Gradien. Kalau kamu ingin belajar persamaan garis singgung lingkaran diketahui gradien secara lebih mendalam, coba simak penjelasan yang ada di sini. Setelah menerima materi, kamu bisa langsung mempraktikkannya dengan mengerjakan latihan soal yang telah kami sediakan. Di sini.
matematika Menentukan Persamaan Garis Singgung Lingkaran
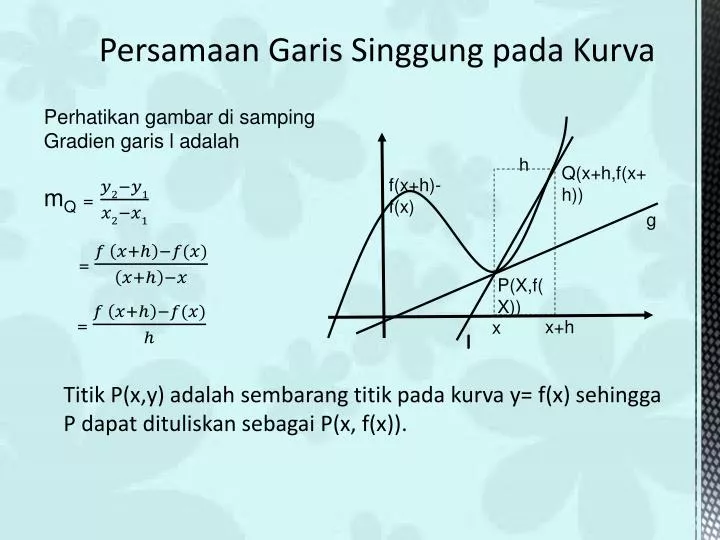
Rumus persamaan garis singgung pada kurva di titik (x1, y1) dengan gradien. Pada postingan ini kita membahas contoh soal persamaan garis singgung yang disertai penyelesaiannya + pembahasan. Lalu apa itu garis singgung ?.. Kemudian hitung x 1 dengan cara subtitusi y = 4 ke persamaan y = x 2 + x - 2 dan diperoleh. 4 = x 2 + x - 2; x 2 + x.
Persamaan Garis Singgung Lingkaran Materi Lengkap Matematika
Tentukan persamaan garis singgung kurva f ( x) = 2 x2 - x + 4 yang melalui x = 1! Pembahasan: Mula-mula, tentukan dahulu nilai f ( x) saat x = 1. Artinya, garis tersebut menyinggung kurva di titik (1, 5). Selanjutnya, tentukan gradien garisnya melalui turunan fungsi. Terakhir, substitusikan ke persamaan garisnya.

Menentukan Persamaan Garis Singgung yang Melalui Titik di Luar Lingkaran YouTube
Menentukan persamaan lingkaran. Persamaan garis singgung lingkaran.. Cukup sekian penjelasan mengenai cara mencari persamaan garis singgung lingkaran berdasarkan gradien garis singgung lingkaran tersebut dalam artikel ini. Semoga bermanfaat. Sumber: Sunardi, Slamet Waluyo & Sutrisna. 2014. Konsep dan Penerapan Matematika SMA/MA Kelas XI.

Menentukan Persamaan Garis Singgung Melalui Sebuah Titik Pada Lingkaran Materi, Soal
Langkah ke-3: Menentukan sebuah persamaan pada garis singgung. Dikarenakan kita mempunyai dua titik singgung, yang tentunya akan terdapat dua persamaan pada garis singgung. Persamaan dari garis singgungnya bagi titik (2,5) dan m = 3. y - y 1 = m (x - x 1) y - 5 = 3 (x - 2) y = 3x - 6 + 5. y = 3x - 1.
PPT Persamaan Garis Singgung pada Kurva PowerPoint Presentation, free download ID6295032
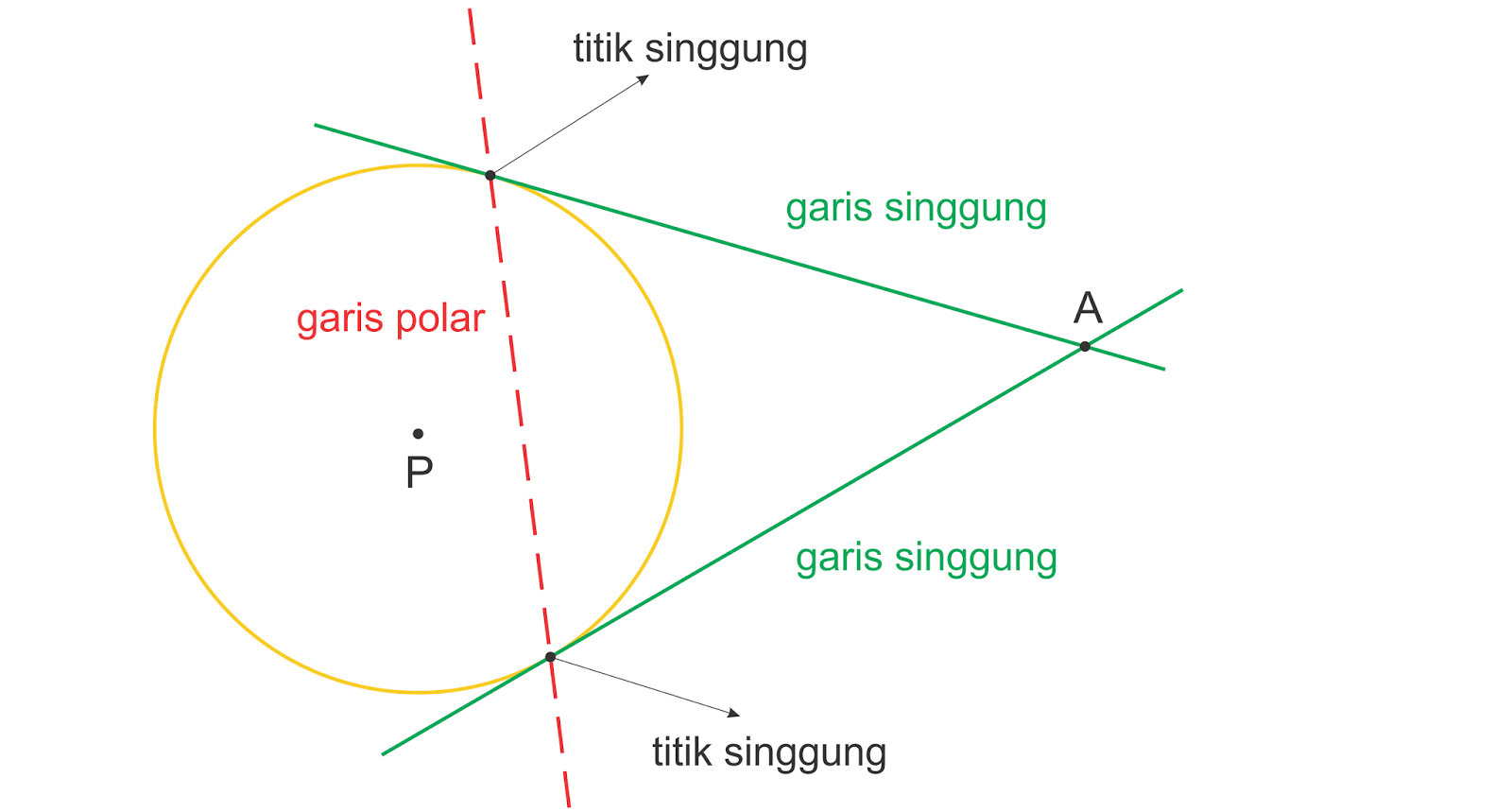
Gambar 1. Garis singgung melalui suatu titik di luar lingkaran. Dari Gambar 1, kita peroleh beberapa hal sebagai berikut: Persamaan garis singgung di titik A(x2,y2) A ( x 2, y 2) pada lingkaran x2 + y2 = r2 x 2 + y 2 = r 2 adalah garis g (garis AP) yang mempunyai persamaan x2x+y2y = r2 x 2 x + y 2 y = r 2. Karena titik P (x1,y1) P ( x 1, y 1.

Contoh Soal Persamaan Garis Singgung Hiperbola Foto Modis
Persamaan Garis singgung lingkaran pusat O(0,0) pada titik . Perhatikan gambar berikut: Persamaan garis singgungnya adalah: Contoh 1: Pembahasan: Pertama kita melakukan uji coba, apakah titik(2,-3. Cara menentukan persamaan garis singgung: Misalkan garis singgungnya y = mx + n;